ลอจิกเกต
เกตพื้นฐานมีทั้งหมด 7 ตัว ได้แก่ OR, AND, NOT, NOR, NAND, XOR และ XNOR เกตที่กล่าวมานี้ไม่ได้เป็นอิสระต่อกัน กล่าวคือเกตบางตัวสามารถสร้างโดยเกตตัวอื่น ๆ ได้ เช่น NOR สามารถสร้างจาก OR ตามด้วย NOT เป็นต้น ในจำนวนเกตพื้นฐานนี้ มีเพียง NAND หรือ NOR ตัวใดตัวหนึ่งก็สามารถสร้างเกตที่เหลือทั้ง 7 ตัวได้ ตัวดำเนินการที่ใส่ไว้เป็นตัวดำเนินการของพีชคณิตแบบบูล
เกต OR
เกต OR คือเกตที่ให้สัญญาณขาออกเป็น 0 เมื่อสัญญาณขาเข้าทุกตัวเป็น 0 และจะให้สัญญาณขาออกเป็น 1 เมื่อสัญญาณขาเข้าตัวใดตัวหนึ่งเป็น 1 เป็นความหมายเดียวกับตรรกะ "หรือ" มีตัวดำเนินการคือ + ตารางค่าความจริงของเกต OR เป็นดังนี้
| A | B | A + B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
เกต NOT
เกต NOT คือเกตที่ให้สัญญาณขาออกเป็นส่วนเติมเต็มของสัญญาณขาเข้า หรือเป็นการสลับค่าของสัญญาณขาเข้า เป็นความหมายเดียวกับตรรกะ "นิเสธ" เกตนี้จะรับสัญญาณขาเข้าเพียงข้างเดียว มีตัวดำเนินการคือ A (อ่านว่า not A หรื A bar) ตารางค่าความจริงของเกต NOT เป็นดังนี้
| A | A |
|---|---|
| 0 | 1 |
| 1 | 0 |
เกต NAND
เกต NAND คือเกตที่ให้สัญญาณขาออกเป็น 0 เมื่อสัญญาณขาเข้าทุกตัวเป็น 1 และจะให้สัญญาณขาออกเป็น 1 เมื่อสัญญาณขาเข้าตัวใดตัวหนึ่งเป็น 0 หรือเป็นส่วนเติมเต็มของเกต AND นั่นเอง ตารางค่าความจริงของเกต NAND เป็นดังนี้
| A | B | A · B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
เกต NOR
เกต NOR คือเกตที่ให้สัญญาณขาออกเป็น 1 เมื่อสัญญาณขาเข้าทุกตัวเป็น 0 และจะให้สัญญาณขาออกเป็น 0 เมื่อสัญญาณขาเข้าตัวใดตัวหนึ่งเป็น 1 หรือเป็นส่วนเติมเต็มของเกต OR นั่นเอง ตารางค่าความจริงของเกต NOR เป็นดังนี้
| A | B | A + B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
เกต XOR (Exclusive OR)
เกต XOR (บางทีก็เรียก เกต EOR) คือเกตที่ให้สัญญาณขาออกเป็น 1 เมื่อสัญญาณขาเข้าต่างกัน และจะให้สัญญาณขาออกเป็น 0 เมื่อสัญญาณขาเข้าเหมือนกัน มีตัวดำเนินการคือ ⊕ ซึ่ง A ⊕ B = (A + B) · (A + B) = A · B + A · B ตารางค่าความจริงของเกต XOR เป็นดังนี้
| A | B | A ⊕ B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
เกต XNOR
เกต XNOR คือเกตที่ให้สัญญาณขาออกเป็น 0 เมื่อสัญญาณขาเข้าต่างกัน และจะให้สัญญาณขาออกเป็น 1 เมื่อสัญญาณขาเข้าเหมือนกัน หรือเป็นส่วนเติมเต็มของเกต XOR นั่นเอง ซึ่ง A ⊕ B = (A + B) · (A + B) = A · B + A · B ตารางค่าความจริงของเกต XNOR เป็นดังนี้
| A | B | A ⊕ B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |









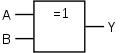



ไม่มีความคิดเห็น:
แสดงความคิดเห็น